[이코테2021] 2강. 그리디 & 구현

- 그리디 알고리즘(탐욕법) : 현재 상황에서 지금 당장 좋은 것만 고르는 방법

- 정당성 분석 중요, 이 방법을 이용해서 문제의 최적의 해를 구할 수 있는지 확인이 중요

 

- 거쳐 가는 노드 값의 합 최대 알고 싶을 때

 

그리디 알고리즘 예시 1

그리디 알고리즘 예시 1

 

- 일반적인 상황에서 그리디 알고리즘은 최적의 해를 보장할 수 없을 때도 많음

- 코테에서는 입력값과 출력값을 정해놓은 경우가 많아서

  대부분의 그리디 문제는 탐욕법으로 얻은 해가 최적의 해가 되는 상황에서, 이를 추론할 수 있어야 풀리도록 출제됨

 

그리디 알고리즘 예시 3

< 문제 해결 아이디어 >

- 최적의 해를 빠르게 구하기 위해서는 가장 큰 화폐 단위부터 돈을 거슬러 주자

- 500, 100, 50, 10 순으로 거슬러줌

ex) N=1260일 때, N이 0원이 될 때까지 500, 100, 50, 10 순서대로 거슬러 주면 됨.

 

- 가장 큰 화폐 단위부터 돈 거슬러주는 게 최적의 해 보장하는 이유는?

가지고 있는 동전에서 큰 단위가 항상 작은 단위의 배수이므로 작은 단위 동전을 종합해 다른 해가 나올 수 없기 때문에

 

그리디 알고리즘은 이처럼 문제 풀이의 최소한 아이디어를 떠올리고 이것이 정당한지 검토해야 한다.

 

<문제> 거스름 돈 : 답안 예시 

 

< 시간 복잡도 분석 >

화폐의 종류가 k라면, O(k)이다.

화폐의 개수 만큼 돌기 때문에, 거슬러 주는 금액과 무관

 

---

 

<문제> 1이 될 때까지

 

<문제> 1이 될 때까지의 조건

 

<문제 해결 아이디어>

- 주어진 N에 대하여 최대한 많이 나누기

=> N의 값을 줄일 때 2이상의 수로 나누는 작업이 1을 빼는 작업보다 수월

 

<정당성 분석>

- N이 아무리 큰 수여도, k로 계속 나누면 기하급수적으로 빠르게 줄이기 가능

- N은 양의 정수이므로 빼기만으로도 항상 1이 되기도 한다. (최적의 해 성립)

 

<문제> 1이 될 때까지

- 기술 : target = ( n // k ) * k

나누어 떨어지지 않더라고 나눌 수 있는 가장 가까운 값을 구할 수 있으므로

- 기술 : result += ( n - target )

result는 1을 빼는 횟수를 몇번 해야하는 지 저장

 

<문제> 곱하기 혹은 더하기

 

- 20억 정수 조건은 int형의 범위 조건을 위해서 있는 것. => python은 필요 없다

 

<문제> 곱하기 혹은 더하기 조건

 

< 문제 해결 아이디어 >

- 대부분의 경우 + 연산자 보다 x 가 더 값을 크게 만든다

- 다만 0이거나 1인 경우는 더하기를 수행

=> 두 수 연산 진행일 시 하나라도 0과 1일 경우 더하기, 나머지는 곱하기 연산자를 하자.

 

<문제> 곱하기 혹은 더하기

 

<문제> 모험가 길드

 

<문제> 모험가 길드 조건

 

<문제> 모함가 길드 조건

 

<문제 해결 아이디어>

- 오름차순 정렬 후 공포도가 낮은 모험가부터 하나씩 확인

- 하나씩 확인하면서 현재 그룹의 모험가의 수가 현재 확인 되고 있는 공포도보다 크거나 같다면 그룹으로 설정

=> 공포도가 오름차순이므로 항상 최소한의 모험가의 수가 포함하여 그룹 결성

 

<문제> 모험가 길드

 

---

 

- 구현 : 머릿속에 있는 알고리즘을 소스코드로 바꾸는 과정

- 알고리즘 대회에서 구현 유형의 문제란 ? 풀이를 떠올리는 것은 쉽지만 소스코드로 옮기기 어려운 문제

1. 알고리즘은 간단한데 코드가 지나칠 만큼 길어지는 문제

2. 실수 연산을 다루고, 특정 소스점 자리까지 출력해야하는 문제

3. 문자열을 특정한 기준에 따라서 끊어 처리해야 하는 문제 => python 용이

4. 적절한 라이브러리를 찾아서 사용해야 하는 문제

 

- 2차원 공간은 행렬(matrix)의 의미

 

행렬(matrix)

 

- 시뮬레이션 및 완전 탐색 문제에서는 2차원 공간에서의 방향 벡터가 자주 활용된다.

ex) 위치 이동

 

방향 벡터

 

<문제> 상하좌우

 

- 가장 왼쪽 위 좌표를 (1,1)이라 하면 리스트 첫 원소를 안쓰거나 혹은 (0,0)인덱스를 (1,1)이라 간주

 

<문제> 상하좌우

 

<문제> 상하좌우 조건

 

<문제 해결 아이디어>

- 요구사항대로 충실히 구현하면 되는 문제

- 일련의 명령에 따라서 개체를 차례대로 이동시킨다는 점에서 시뮬레이션(simulation) 유형으로 분류

- 시뮬레이션 유형, 구형 유형, 완전 탐색 유형은 서로 유사하다는 점

 

<문제> 상하좌우

 

- nx와 ny를 if 안에서 초기화 하고나서 바깥 반복문에서도 사용 가능하다

 

---

 

<문제> 시각

 

<문제> 시각 조건

 

<문제 해결 아이디어>

- 이 문제는 모든 시각 경우를 하나씩 모두 세서 풀 수 있는 문제 (완전탐색 문제)

- 하루는 24*60*60 = 86400 초이므로 컴퓨터 계산 가능

- python은 1초에 2천만번 계산 가능하다고 가정하고 생각하면 완전탐색 가능 확인

- 완전 탐색(brute forcing) 문제 유형 : 가능한 경우의 수를 모두 검사해보는 탐색 방법

 

<문제> 시각

- 3이 들어 있는지 확인할 때 파이썬 기술 : in 활용

 

<문제> 왕실의 나이트

<문제> 왕실의 나이트

 

<문제> 왕실의 나이트

 

<문제> 왕실의 나이트 조건

 

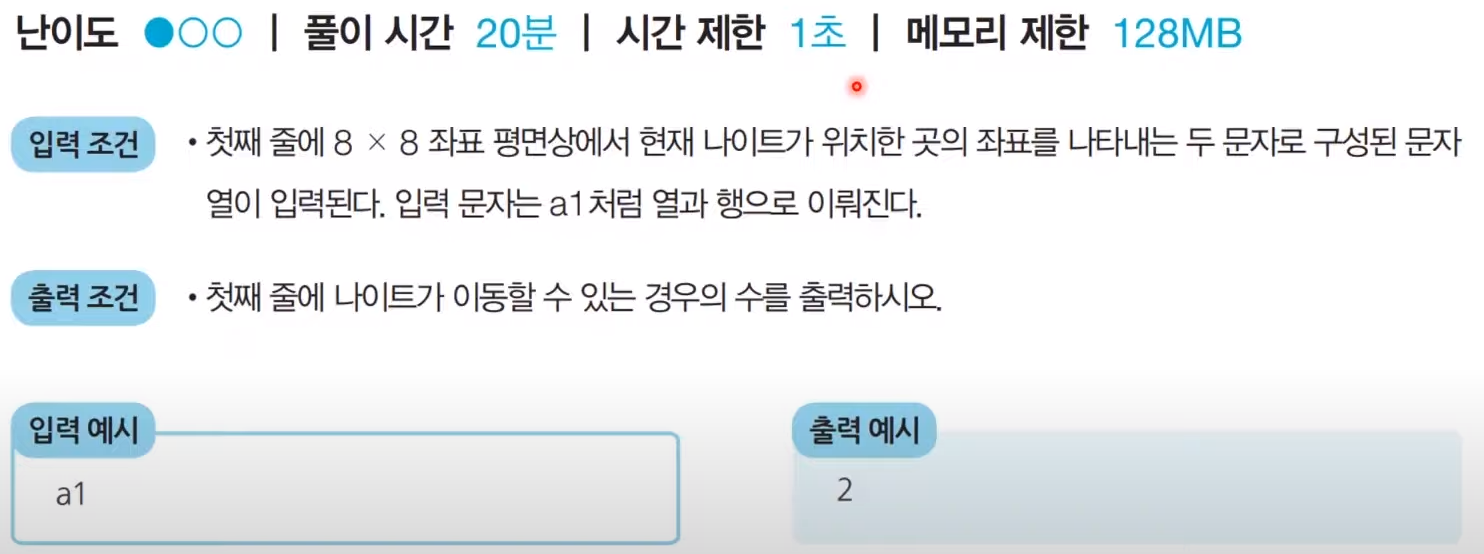
<문제 해결 아이디어>

- 요구사항대로 충실히 구현하면 되는 문제

- 나이트의 8가지 경로를 하나씩 확인하며 각 위치로 이동 가능한지 확인하자

 

<문제> 왕실의 나이트

- 직접 list안에 좌표 형태로도 저장 가능

 

 

<문제> 문자열 재정렬

<문제> 문자열 재정렬

 

<문제 해결 아이디어>

- 요구사항대로 충실히 구현하면 되는 문제

- 문자열이 입력되었을 때 문자를 하나씩 확인

1. 숫자인 경우 따로 합계 계산

2. 알파벳인 경우 별도의 리스트에 저장

=> 리스트에 저장되 ㄴ알파벳을 정렬해 출력하고, 합계를 뒤에 붙여 출력하면 정답

 

<문제> 문자열 재정렬